บทที่8
การเรียงลำดับ ( Sorting )
ในชีวิตประจำวันเราได้มีการจัดเรียงข้อมูลต่างๆ มากมายหลายอย่าง เช่นการจัดเรียงตัวอักษรในพจนานุกรม การเรียงลำดับรายชื่อที่มีคะแนนสูงสุดไปต่ำสุด การจัดเรียงรายชื่อในสมุดโทรศัพท์ ฯลฯ เหตุที่ทำให้ต้องมีการจัดเรียงข้อมูลก็เพราะว่าง่ายต่อการค้นหาและตีความ ซึ่งเราจะข้อมูลนั้นไปใช้ในการกระทำอย่างอื่น ในคอมพิวเตอร์ก็เช่นเดียวกัน ถ้าหากมีข้อมูลมาก ๆ แล้วไม่ทำการเรียงข้อมูล ก็จะทำให้เสียเวลาในการค้นหาข้อมูลเป็นอย่างมาก เราจึงต้องมีการเรียงข้อมูลกันก่อนที่จะดึงข้อมูลมาใช้ เพื่อจะได้สะดวกในการเขียนโปรแกรม การค้นหาข้อมูล และเสียเวลาน้อยลง ดังนั้นเราจะต้องมาศึกษากันถึงวิธีการเรียงข้อมูลในระบบคอมพิวเตอร์ว่ามีวิธีอย่างไรบ้าง
ประเภทของการจัดเรียงลำดับข้อมูล
การจัดเรียงลำดับข้อมูลในระบบคอมพิวเตอร์ สามารถแบ่งออกได้เป็น 2 ประเภทใหญ่ๆ คือ
1. การจัดเรียงลำดับภายใน (Internal Sorting) เป็นการจัดเรียงลำดับข้อมูลที่เก็บอยู่ในหน่วยความจำ โดยข้อมูลเหล่านี้จะถูกเก็บอยู่ในโครงสร้างข้อมูลแบบอาร์เรย์ หรือลิงค์ลิสท์ ข้อมูลที่ทำการเรียงลำดับมีขนาดเล็กหรือจำนวนไม่มาก ซึ่งหน่วยความจำสามารถจะอ่านข้อมูลทั้งหมดขึ้นมาบนหน่วยความจำ และสามารถทำงานต่างๆ บนหน่วยความจำได้โดยไม่ต้องอาศัยสื่อบันทึกข้อมูล เช่น ดิสก์ หรือ เทป มาช่วยในการทำงาน ประสิทธิภาพของการจัดเรียงในลักษณะนี้ เน้นที่การสลับหรือเคลื่อนย้ายข้อมูลให้น้อยที่สุด จะทำให้ความเร็วของโปรแกรมดีขึ้น
2. การจัดเรียงลำดับภายนอก (External Sorting) เป็นการจัดเรียงลำดับข้อมูลที่เก็บอยู่ในสื่อบันทึกข้อมูล โดยทั่วไปข้อมูลที่บันทึกนี้ มักมีจำนวนมากจนไม่สามารถจะเก็บเอาไว้ในหน่วยความจำได้ทั้งหมด ต้องแบ่งออกเป็นส่วนย่อยๆ แล้วจึงนำมาจัดเรียงในหน่วยความจำ จากนั้นจึงทำการบันทึกกลับลงไปในสื่อสำหรับบันทึกข้อมูลเป็นส่วนๆ ต่อจากนั้นนำส่วนต่างๆ ที่จัดเรียงลำดับเรียบร้อยแล้วมาทำการรวมเข้าด้วยกัน (Merge) สำหรับการเรียงแบบภายนอกนั้น จะต้องคิดถึงเวลาที่สูญเสียไปอันเนื่องจากการถ่ายเทข้อมูลระหว่างเทปหรือดิสก์ กับหน่วยความจำหลักด้วย เวลาที่สูญเสียไปในการถ่ายเทข้อมูลระหว่างหน่วยความจำหลักกับเทป หรือดิสก์จะเป็นตัวระบุความดีเลวของแบบการคำนวณแบบเรียงภายนอก
การเรียงลำดับแบบเลือก (selection sort)
ทำการเลือกข้อมูลมาเก็บในตำแหน่งที่ข้อมูลนั้นควรจะอยู่ทีละตัวโดยทำการค้นหาข้อมูลนั้นในแต่ละรอบแบบเรียงลำดับถ้าเป็นการเรียงลำดับจากน้อยไปมาก
1. ในรอบแรกจะทำการค้นหาข้อมูลตัวที่มีค่าน้อยที่สุดมาเก็บไว้ที่ตำแหน่งที่ 1
2. ในรอบที่สองนำข้อมูลตัวที่มีค่าน้อยรองลงมาไปเก็บไว้ที่ตำแหน่งที่สอง
3. ทำเช่นนี้ไปเรื่อย ๆ จนกระทั่งครบทุกค่าในที่สุดจะได้ข้อมูลเรียงลำดับจากน้อยไปมากตามที่ต้องการ
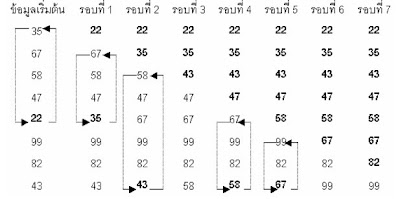
ในรอบที่ 1 ทำการเปรียบเทียบข้อมูลเพื่อค้นหาข้อมูลที่มีค่าน้อยที่สุด คือ 22นำไปวางที่ตำแหน่งที่ 1 สลับตำแหน่งกับ 35ในรอบที่ 2 ทำการเปรียบเทียบอีกเพื่อค้นหาค่าที่น้อยที่สุดรองลงมาโดยเริ่มค้นตั้งแต่ตำแหน่งที่ 2 เป็นต้นไปได้ค่าน้อยที่สุดคือ 35นำไปวางที่ตำแหน่งที่ 2 สลับตำแหน่งกับ 67ในรอบต่อไปก็ทำในทำนองเดียวกันจนกระทั่งถึงรอบสุดท้ายคือรอบที่ 7 จะได้ข้อมูลที่เรียงลำดับจากน้อยไปมากตามที่ต้องการการจัดเรียงลำดับแบบเลือกเป็นวิธีที่ง่ายและตรงไปตรงมา แต่มีข้อเสียตรงที่ใช้เวลาในการจัดเรียงนานเพราะแต่ละรอบต้องเปรียบเทียบกับข้อมูลทุกตัว ถ้ามีจำนวนข้อมูลทั้งหมด n ตัว ต้องทำการเปรียบเทียบทั้งหมดรอบเป็นดังนี้รอบที่ 1 เปรียบเทียบเท่ากับ n −1 ครั้งรอบที่ 2 เปรียบเทียบเท่ากับ n – 2 ครั้ง
...
รอบที่ n – 1 เปรียบเทียบเท่ากับ 1 ครั้งn – 1 รอบ และจำนวนครั้งของการเปรียบเทียบในแต่ละจำนวนครั้งของการเปรียบเทียบทั้งหมด
= (n −1) + (n −2) + . . . + 3 + 2 + 1
= n (n −1) / 2 ครั้ง
...
รอบที่ n – 1 เปรียบเทียบเท่ากับ 1 ครั้งn – 1 รอบ และจำนวนครั้งของการเปรียบเทียบในแต่ละจำนวนครั้งของการเปรียบเทียบทั้งหมด
= (n −1) + (n −2) + . . . + 3 + 2 + 1
= n (n −1) / 2 ครั้ง
การเรียงลำดับแบบฟอง (Bubble Sort)
เป็นวิธีการเรียงลำดับที่มีการเปรียบเทียบข้อมูลในตำแหน่งที่อยู่ติดกัน
1. ถ้าข้อมูลทั้งสองไม่อยู่ในลำดับที่ถูกต้องให้สลับตำแหน่งที่อยู่กัน
2. ถ้าเป็นการเรียงลำดับจากน้อยไปมากให้นำข้อมูลตัวที่มีค่าน้อยกว่าอยู่ในตำแหน่งก่อนข้อมูลที่มีค่ามาก ถ้าเป็นการเรียงลำดับจากมากไปน้อยให้นำข้อมูล ตัวที่มีกำหนดให้มีข้อมูล n จำนวน การเปรียบเทียบเริ่มจากคู่แรกหรือคู่สุดท้ายก็ได้ ถ้าเริ่มจากคู่สุดท้ายจะเปรียบเทียบข้อมูลที่ตำแหน่ง n-1 กับ n ก่อนแล้วจัดเรียงให้อยู่ในตำแหน่งที่ถูกต้อง ต่อไปเปรียบเทียบข้อมูลที่ตำแหน่ง n-2 กับ n-1 ทำเช่นนี้ไป เรื่อย ๆจนกระทั่งถึงข้อมูลตัวแรก และทำการเปรียบเทียบในรอบอื่นเช่นเดียวกันจนกระทั่งถึงรอบสุดท้ายที่เหลือข้อมูล 2 ตำแหน่งสุดท้าย เมื่อการจัดเรียงเสร็จเรียบร้อยทุกตำแหน่งก็จะได้ข้อมูลเรียงลำดับตามที่ ต้องการ
1. ถ้าข้อมูลทั้งสองไม่อยู่ในลำดับที่ถูกต้องให้สลับตำแหน่งที่อยู่กัน
2. ถ้าเป็นการเรียงลำดับจากน้อยไปมากให้นำข้อมูลตัวที่มีค่าน้อยกว่าอยู่ในตำแหน่งก่อนข้อมูลที่มีค่ามาก ถ้าเป็นการเรียงลำดับจากมากไปน้อยให้นำข้อมูล ตัวที่มีกำหนดให้มีข้อมูล n จำนวน การเปรียบเทียบเริ่มจากคู่แรกหรือคู่สุดท้ายก็ได้ ถ้าเริ่มจากคู่สุดท้ายจะเปรียบเทียบข้อมูลที่ตำแหน่ง n-1 กับ n ก่อนแล้วจัดเรียงให้อยู่ในตำแหน่งที่ถูกต้อง ต่อไปเปรียบเทียบข้อมูลที่ตำแหน่ง n-2 กับ n-1 ทำเช่นนี้ไป เรื่อย ๆจนกระทั่งถึงข้อมูลตัวแรก และทำการเปรียบเทียบในรอบอื่นเช่นเดียวกันจนกระทั่งถึงรอบสุดท้ายที่เหลือข้อมูล 2 ตำแหน่งสุดท้าย เมื่อการจัดเรียงเสร็จเรียบร้อยทุกตำแหน่งก็จะได้ข้อมูลเรียงลำดับตามที่ ต้องการ

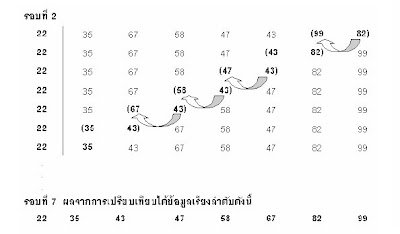
จากตัวอย่าง การเปรียบเทียบจะเริ่มเปรียบเทียบจากคู่หลัง ในรอบที่ 1 เปรียบเทียบข้อมูลที่ตำแหน่งที่ 7 กับ 8 ได้ว่า 43 น้อยกว่า 82 ให้ทำการสลับตำแหน่งกันเพื่อให้ค่าที่น้อยกว่าอยู่ก่อนต่อไปเปรียบเทียบข้อมูลตำแหน่งที่ 6 กับ 7 ได้ว่า43 น้อยกว่า 99 ให้ทำการสลับตำแหน่งกันอีก ทำการเปรียบเทียบเช่นนี้ในคู่ต่อไปเรื่อย ๆ จนกระทั่งในรอบที่ 2 ทำการเปรียบเทียบข้อมูลจากคู่หลังมาคู่หน้าเช่นกัน แต่จะเปรียบเทียบถึงตำแหน่งที่ 2เท่านั้นจนกระทั่งได้ค่าต่ำสุดรองลงมาไว้ในตำแหน่งที่ 2 ในรอบต่อไปก็ทำในทำนองเดียวกันจนกระทั่งถึงรอบสุดท้ายคือรอบที่ 7 จะเหลือข้อมูลที่ต้องเปรียบเทียบคู่เดียวคือข้อมูลในตำแหน่งที่ 7 กับ 8เมื่อการจัดเรียงเสร็จเรียบร้อยเราจะได้ข้อมูลที่มีการเรียงลำดับจากน้อยไปมากตามที่ต้องการการจัดเรียงลำดับแบบฟองเป็นวิธีที่ไม่ซับซ้อนมากนัก เป็นวิธีการเรียงลำดับที่นิยมใช้กันมากเพราะมีรูปแบบที่เข้าใจง่าย แต่ประสิทธิภาพการทำงานค่อนข้างต่ำพอ ๆ กับการเรียงลำดับแบบเลือกในหัวข้อที่ผ่านมาถ้ามีจำนวนข้อมูลทั้งหมด n ตัวไม่ว่าข้อมูลเป็นอย่างไรก็ตามต้องทำการเปรียบเทียบทั้งหมด n −1 รอบ และจำนวนครั้งของการเปรียบเทียบในแต่ละรอบเป็นดังนี้
กรณีที่แย่ที่สุดจำนวนครั้งของการเปรียบเทียบดังนี้
รอบที่ 1 เปรียบเทียบเท่ากับ n − 1 คู่
รอบที่ 2 เปรียบเทียบเท่ากับ n − 2 คู่
...
รอบที่ n −1 เปรียบเทียบเท่ากับ 1 คู่จำนวนครั้งของการเปรียบเทียบ
= (n −1) + (n −2) + . . . + 3 + 2 + 1
= n (n −1) / 2 ครั้ง
กรณีที่แย่ที่สุดจำนวนครั้งของการเปรียบเทียบดังนี้
รอบที่ 1 เปรียบเทียบเท่ากับ n − 1 คู่
รอบที่ 2 เปรียบเทียบเท่ากับ n − 2 คู่
...
รอบที่ n −1 เปรียบเทียบเท่ากับ 1 คู่จำนวนครั้งของการเปรียบเทียบ
= (n −1) + (n −2) + . . . + 3 + 2 + 1
= n (n −1) / 2 ครั้ง
กรณีที่ดีที่สุด
คือ กรณีที่ข้อมูลมีการเรียงลำดับในตำแหน่งที่ถูกต้องอยู่แล้ว โดยจะทำการเปรียบเทียบในรอบที่ 1 รอบเดียวเท่านั้น ก็สามารถสรุปได้ว่าข้อมูลเรียงลำดับเรียบร้อยแล้ว ถ้ามีจำนวนข้อมูลทั้งหมด n จำนวนจำนวนครั้งของการ
คือ กรณีที่ข้อมูลมีการเรียงลำดับในตำแหน่งที่ถูกต้องอยู่แล้ว โดยจะทำการเปรียบเทียบในรอบที่ 1 รอบเดียวเท่านั้น ก็สามารถสรุปได้ว่าข้อมูลเรียงลำดับเรียบร้อยแล้ว ถ้ามีจำนวนข้อมูลทั้งหมด n จำนวนจำนวนครั้งของการ
การเรียงลำดับแบบเร็ว (quick sort)
เป็นวิธีการเรียงลำดับที่ใช้เวลาน้อยเหมาะสำหรับข้อมูลที่มีจำนวนมากที่ต้องการความรวดเร็วในการทำงาน วิธีนี้จะเลือกข้อมูลจากกลุ่มข้อมูลขึ้นมาหนึ่งค่าเป็นค่าหลัก แล้วหาตำแหน่งที่ถูกต้องให้กับค่าหลักนี้ เมื่อได้ตำแหน่งที่ถูกต้องแล้ว ใช้ค่าหลักนี้เป็นหลักในการแบ่งข้อมูลออกเป็นสองส่วนถ้าเป็นการเรียงลำดับจากน้อยไปมาก ส่วนแรกอยู่ในตอนหน้าข้อมูล ทั้งหมดจะมีค่าน้อยกว่าค่าหลักที่เป็นตัวแบ่งส่วนอีกส่วนหนึ่งจะอยู่ในตำแหน่งตอนหลังข้อมูลทั้งหมด จะมีค่ามากกว่าค่าหลัก แล้วนำแต่ละส่วนย่อยไปแบ่งย่อยในลักษณะเดียวกันต่อไปจนกระทั่งแต่ละส่วนไม่สามารถแบ่งย่อยได้อีกต่อไปจะได้ข้อมูลที่มีการเรียงลำดับตามที่ต้องการถ้าเป็นการเรียงลำดับจากน้อยไปมากการเปรียบเทียบเพื่อหาตำแหน่งให้กับค่าหลักตัวแรกเริ่มจากข้อมูลในตำแหน่งแรกหรือสุดท้ายก็ได้ ถ้าเริ่มจากข้อมูลที่ตำแหน่งที่ 1เป็นค่าหลัก พิจารณาเปรียบเทียบค่าหลักกับข้อมูลในตำแหน่งสุดท้าย ถ้าค่าหลักมีค่าน้อยกว่าให้เปรียบเทียบกับข้อมูลในตำแหน่งรองสุดท้ายไปเรื่อย ๆ จนกว่าจะพบค่าที่น้อยกว่าค่าหลักแล้วให้สลับตำแหน่งกันหลังจากสลับตำแหน่งแล้วนำค่าหลักมาเปรียบเทียบกับข้อมูล ในตำแหน่งที่ 2, 3,ไปเรื่อย ๆ จนกว่าจะพบค่าที่มากกว่าค่าหลักสลับตำแหน่งเมื่อเจอข้อมูลที่มากกว่าค่าหลัก ทำเช่นนี้ไปเรื่อย ๆ จนกระทั่งได้ตำแหน่งที่ถูกต้องของค่าหลักนั้น ก็จะแบ่งกลุ่มข้อมูลออกเป็นสองส่วน ส่วนแรกข้อมูลทั้งหมดมีค่าน้อยกว่าค่าหลักและส่วนที่สองข้อมูลทั้งหมดมีค่ามากกว่าค่า

จากการเปรียบเทียบข้างต้นในที่สุดก็ได้ตำแหน่งที่วางค่าหลัก 44 ซึ่งข้อมูลจะถูกแบ่งเป็น 2 ส่วน ส่วนที่ 1 ข้อมูลทั้งหมดมีค่าน้อยกว่าค่าหลัก และส่วนที่ 2 ข้อมูลทั้งหมดมีค่ามากกว่าค่าหลัก นำแต่ละส่วนไปดำเนินการเปรียบเทียบในลักษณะเดียวกันจนกระทั่งข้อมูลทั้งหมดเรียงลำดับจากน้อยไปมากตามต้องการการจัดเรียงลำดับแบบเร็วเป็นวิธีที่ค่อนข้างซับซ้อน แต่ประสิทธิภาพการทำงานค่อนสูง เนื่องจากใช้เวลาในการเรียงลำดับน้อย ถ้ามีข้อมูลทั้งหมด n ตัวจำนวนครั้งของการเปรียบเทียบเป็นดังนี้ กรณีที่ดีที่สุด คือ กรณีที่ค่าหลักที่เลือกแบ่งแล้วข้อมูลอยู่ตรงกลางกลุ่มพอดี และในแต่ละส่วนย่อยก็เช่นเดียวกันจำนวนครั้งของการเปรียบเทียบเป็นดังนี้จำนวนครั้งของการเปรียบเทียบ = n log2 n ครั้ง
กรณีที่แย่ที่สุด คือ กรณีที่ข้อมูลมีการเรียงลำดับอยู่แล้ว อาจจะเรียงจากน้อยไปมากหรือจากมากไปน้อย หรือค่าหลักที่เลือกในแต่ละครั้งเป็นค่าหลักที่น้อยที่สุดหรือมากที่สุด จำนวนครั้งของการเปรียบเทียบจะมากที่สุดดังนี้จำนวนครั้งของการเปรียบเทียบ
= (n −1) + (n −2) + . . . + 3 + 2 + 1
= n (n −1) / 2 ครั้ง
= (n −1) + (n −2) + . . . + 3 + 2 + 1
= n (n −1) / 2 ครั้ง
การเรียงลำดับแบบแทรก (insertion sort)
เป็นวิธีการเรียงลำดับที่ทำการเพิ่มสมาชิกใหม่เข้าไปในเซต ที่มีสมาชิกทุกตัวเรียงลำดับอยู่แล้ว และทำให้เซตใหม่ที่ได้นี้มีสมาชิกทุกตัวเรียงลำดับด้วย วิธีการเรียงลำดับจะ
1. เริ่มต้นเปรียบเทียบจากข้อมูลในตำแหน่งที่ 1 กับ 2หรือข้อมูลในตำแหน่งสุดท้ายและรองสุดท้ายก็ได้ถ้าเป็นการเรียงลำดับจากน้อยไปมาก
2. จะต้องจัดให้ข้อมูลที่มีค่าน้อยอยู่ในตำแหน่งก่อนข้อมูลที่มีค่ามาก และถ้าเรียงจากมากไปน้อยจะก็จะจัดให้ข้อมูลที่มีค่ามากอยู่ในตำแหน่งก่อน
1. เริ่มต้นเปรียบเทียบจากข้อมูลในตำแหน่งที่ 1 กับ 2หรือข้อมูลในตำแหน่งสุดท้ายและรองสุดท้ายก็ได้ถ้าเป็นการเรียงลำดับจากน้อยไปมาก
2. จะต้องจัดให้ข้อมูลที่มีค่าน้อยอยู่ในตำแหน่งก่อนข้อมูลที่มีค่ามาก และถ้าเรียงจากมากไปน้อยจะก็จะจัดให้ข้อมูลที่มีค่ามากอยู่ในตำแหน่งก่อน
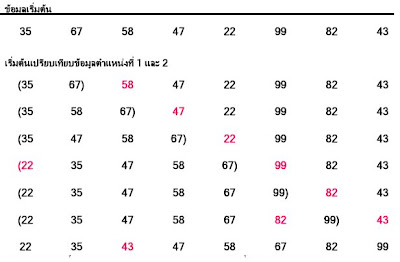
ถ้ามีจำนวนข้อมูลเป็น n การจัดเรียงแบบแทรกจะมีการจัดเรียงทั้งหมดเท่ากับ n − 1 รอบ จำนวนครั้งของการเปรียบเทียบในแต่ละรอบแตกต่างกันขึ้นอยู่กับลักษณะการจัดเรียงของข้อมูลนั้น กรณีที่ดีที่สุด คือ กรณีข้อมูลทั้งหมดจัดเรียงในตำแหน่งที่ต้องการเรียบร้อยแล้ว กรณีนี้ในแต่ละรอบมีการเปรียบเทียบเพียงครั้งเดียว เพราะฉะนั้นจำนวนครั้งของการเปรียบเทียบเป็นดังนี้จำนวนครั้งของการเปรียบเทียบ = n − 1 ครั้ง
กรณีที่แย่ที่สุด คือ กรณีที่ข้อมูลมีการเรียงลำดับในตำแหน่งที่กลับกัน เช่น ต้องการเรียงลำดับจากน้อยไปมาก แต่ข้อมูลมีค่าเรียงลำดับจากมากไปน้อย จำนวนครั้งของการเปรียบเทียบในแต่ละรอบดังนี้
ในรอบที่ 1 จำนวนครั้งของการเปรียบเทียบเป็น 1 ครั้ง
ในรอบที่ 2 จำนวนครั้งของการเปรียบเทียบเป็น 2 ครั้ง
จำนวนครั้งของการเปรียบเทียบ
= 1 + 2 + 3 + . . . +(n −2) + (n −1)
= n (n −1) / 2
ในรอบที่ 1 จำนวนครั้งของการเปรียบเทียบเป็น 1 ครั้ง
ในรอบที่ 2 จำนวนครั้งของการเปรียบเทียบเป็น 2 ครั้ง
จำนวนครั้งของการเปรียบเทียบ
= 1 + 2 + 3 + . . . +(n −2) + (n −1)
= n (n −1) / 2
การจัดเรียงลำดับแบบฮีพ(HEAP SORT)
การเรียงข้อมูลโดยอาศัยโครงสร้าง Heap เป็นการเรียงข้อมูลแบบที่ดีที่สุด เพราะเป็น อัลกอริทึมที่ประกันได้ว่าเวลาที่ใช้ไม่ว่าในกรณีใดจะเป็น O(log 2 n) เสมอ โครงสร้าง Heap heap เป็นต้นไม้ไบนารีที่มีคุณสมบัติว่าโหนดใด ๆ ในต้นไม้นั้นจะมีค่าคีย์ใหญ่กว่าค่าคีย์ที่อยู่ใน left son และ right son ของมัน (ถ้าโหนดนั้นมีลูก) ตัวอย่างดังรูป (ก) เป็น heap ส่วนรูป (ข) ไม่ใช่ heap
รูป การเปรียบเทียบระหว่างโครงสร้าง Heap กับโครงสร้างอื่น
ขั้นที่ 1 สร้างโครงสร้าง heap
ขั้นที่ 2 เอาต์พุตคีย์ที่รูตโหนด
ขั้นที่ 3 ปรับแต่งต้นไม่ที่เหลือให้เป็น heap
การสร้างโครงสร้าง Heap จากชุดอินพุต อาร์เรย์ใด ๆ สามารถถูกตีความเป็นต้นไม้ไบนารีได้ เช่น อาร์เรย์ที่มีค่าดังนี้
ความสัมพันธ์ระหว่างโครงสร้างอาร์เรย์และโครงสร้าง Heap จะมีรูปเป็นต้นไม้ไบนารีดังรูป
รูปต้นไม้ไบนารีของอาร์เรย์
ขั้นที่ 1 ให้เปรียบเทียบโหนดที่เข้าใหม่กับโหนดที่เป็นพ่อ
IF Knew > K FATHER THEN แลกที่กัน เลื่อน I ไปชี้ยังตำแหน่ง FATHER (นั่นคือ I ติดตาม Knew ขึ้นไป)
ขั้นที่ 2 ทำขั้นที่ 1 เรื่อย ๆ จนทำไม่ได้
ต้นไม้ที่เห็นระหว่างการสร้าง heap นั้น เป็นการตีความข้อมูลในอาร์เรย์ ส่วนความสัมพันธ์ระหว่างพ่อ - ลูก เป็นแบบที่กล่าวมาแล้วข้างต้น หลังจากที่ข้อมูลเรียงในรูปโครงสร้าง heap แล้ว เราจะเอาเอาต์พุตค่ารูตโหนดซึ่งอยุ่ที่ตำแหน่งที่ 1 ในอาร์เรย์ การเอาต์พุตเราจะให้ค่าA(1) แลกที่กับค่าสุดท้ายของอาร์เรย์ A(8) การแทนในรูปต้นไม้ ค่าที่เอาต์พุตไปแล้วจะแทนโดยโหนดสี่เหลี่ยม ต้นไม้ที่ได้ (ไม่นับโหนดสี่เหลี่ยม) ไม่เป็นโครงสร้าง heap จากนี้ต่อไปเราต้องใช้อัลกอริทึมปรับค่าคีย์ต่าง ๆ ในต้นไม้ให้คุณสมบัติ heap การปรับต้นไม้ที่ได้จากการแลกค่าให้มีคุณสมบัติ Heap การปรับแต่งทำได้โดยเลื่อนค่าที่รูตโหนดจากบนลงมาล่าง ดังนี้
ขั้นที่ 1 ให้ตั้งค่าพอยน์เตอร์ I ชี้ไปยังรูตโหนด
ขั้นที่ 2 ให้เลือกค่าที่ใหญ่ที่สุดระหว่าง left son และ right sonของโหนด I เป็นค่าที่เลื่อนมาอยู่ที่ตำแหน่ง I ส่วนค่าคีย์ที่ตำแหน่ง I ก็เลื่อนไปอยู่ที่ตำแหน่ง left son และ right son ของมันที่มีค่าใหญ่กว่า จากนั้นเลื่อนพอยน์เตอร์ I มาอยู่ที่ตำแหน่งใหม่นี้
ขั้นที่ 3 ทำขั้นที่ 2 จนกว่าจะทำไม่ได้
ขั้นที่ 1 ให้ตั้งค่าพอยน์เตอร์ I ชี้ไปยังรูตโหนด
ขั้นที่ 2 ให้เลือกค่าที่ใหญ่ที่สุดระหว่าง left son และ right sonของโหนด I เป็นค่าที่เลื่อนมาอยู่ที่ตำแหน่ง I ส่วนค่าคีย์ที่ตำแหน่ง I ก็เลื่อนไปอยู่ที่ตำแหน่ง left son และ right son ของมันที่มีค่าใหญ่กว่า จากนั้นเลื่อนพอยน์เตอร์ I มาอยู่ที่ตำแหน่งใหม่นี้
ขั้นที่ 3 ทำขั้นที่ 2 จนกว่าจะทำไม่ได้
รูปการปรับต้นไม้ให้มีคุณสมบัติ Heap
ประเภทของ Heap จะมีอยู่ 2 ประเภท คือ
1. Max heap คือ ประเภทของโหนดลูกแต่ละโหนดจะเก็บข้อมูลที่มีค่าน้อยกว่าหรือเท่ากับข้อมูลใน โหนดพ่อโดยเฉพาะข้อมูลที่ตำแหน่งรูตโหนดจะมีค่ามากที่สุด
2. Min heap คือ โหนดลูกแต่ละโหนดจะเก็บข้อมูลที่มีค่ามากกว่าหรือเท่ากับข้อมูลในโหนดพ่อแม่ โดยเฉพาะข้อมูลที่ตำแหน่งรูตโหนดจะมีค่าน้อยที่สุด
เงื่อนไขของการแตกกิ่งก้านสาขาของโหนด คือ
1. ทุกระดับชั้นของ heap จะแตกสาขาออกได้สองทางคือ ซ้ายและขวา การแตกโหนดจะแตกจากทางซ้ายก่อน และต้องมีโหนดในระดับรูตโหนดครบ 2 ด้านก่อนจึงจะแตกโหนดต่อไปในระดับล่างได้
2. ค่าของโหนดที่เป็นรูตโหนดของ heap จะเป็นโหนดที่มีค่าใหญ่กว่าโหนดตัวล่าง
การสร้าง Heap
จากนิยามของโครงสร้าง heap เราทราบว่ารูตโหนดของ heap จะเป็นโหนดที่มีค่าคีย์ใหญ่กว่า ดังนั้นจากอันพุตที่กำหนดให้เราต้องสร้าง heap ขึ้นก่อน แล้วทำการเอาต์พุตรูตโหนดก็จะได้ค่าแรก (ค่าใหญ่ที่สุด) ของชุดที่เรียงแล้ว ในกรณีนี้จะเรียงจากมากไปน้อย(อัลกอริทึมที่เราอธิบายถึงจะได้ค่าที่เรียง แล้วจากน้อยไปมาก) หลังจากที่เอาต์พุตค่ารูตโหนดไปแล้ว ต้นไม่ที่เหลืออยู่จะไม่เป็น heap เราต้องมีวิธีการตกแต่งหรือปรับแต่งให้ต้นไม้ที่เหลืออยู่นั้นเป็น heap จะได้เอาต์พุตค่าถัดไปได้ ดังนั้นกระบวนการใหญ่ของการทำ heap sort ประกอบด้วย 3 ขั้นตอนดังนี้
ขั้นที่ 1 สร้างโครงสร้าง heap
ขั้นที่ 2 เอาต์พุตคีย์ที่รูตโหนด
ขั้นที่ 3 ปรับแต่งต้นไม่ที่เหลือให้เป็น heap
ขั้นที่ 1 สร้างโครงสร้าง heap
ขั้นที่ 2 เอาต์พุตคีย์ที่รูตโหนด
ขั้นที่ 3 ปรับแต่งต้นไม่ที่เหลือให้เป็น heap
ตัวอย่าง ข้อมูลเริ่มต้นของฮีพ
2. สลับ 36 กับ 2
3. สลับ 25 กับ 1
4. สลับ 19 กับ 2
5. สลับ 17 กับ 2
6. สลับ 7 กับ 1
7. สลับ 3 กับ 2
8. สลับ 2 กับ 1
วิธีการเรียงลำดับแบบฮีพ โดยแทนฮีพพด้วย Array แสดงในรูป
[1]
|
[2]
|
[3]
|
[4]
|
[5]
|
[6]
|
[7]
|
[8]
|
[9]
| |
ฮีพเริ่มต้น
|
100
|
19
|
36
|
17
|
3
|
25
|
1
|
2
|
7
|
1. สลับ 100 กับ 7
|
7
|
19
|
36
|
17
|
3
|
25
|
1
|
2
|
100
|
ปรับฮีพ
|
36
|
19
|
25
|
17
|
3
|
7
|
1
|
2
|
100
|
2. สลับ 36 กับ 2
|
2
|
19
|
25
|
17
|
3
|
7
|
1
|
36
|
100
|
ปรับฮีพ
|
25
|
19
|
7
|
17
|
3
|
2
|
1
|
36
|
100
|
3. สลับ 25 กับ 1
|
1
|
19
|
7
|
17
|
3
|
2
|
25
|
36
|
100
|
ปรับฮีพ
|
19
|
17
|
7
|
1
|
3
|
2
|
25
|
36
|
100
|
4. สลับ 19 กับ 2
|
2
|
17
|
7
|
1
|
3
|
19
|
25
|
36
|
100
|
ปรับฮีพ
|
17
|
3
|
7
|
1
|
2
|
19
|
25
|
36
|
100
|
5. สลับ 17 กับ 2
|
2
|
3
|
7
|
1
|
17
|
19
|
25
|
36
|
100
|
ปรับฮีพ
|
7
|
3
|
2
|
1
|
17
|
19
|
25
|
36
|
100
|
6. สลับ 7 กับ 1
|
1
|
3
|
2
|
7
|
17
|
19
|
25
|
36
|
100
|
ปรับฮีพ
|
3
|
1
|
2
|
7
|
17
|
19
|
25
|
36
|
100
|
7. สลับ 3 กับ 2
|
2
|
1
|
3
|
7
|
17
|
19
|
25
|
36
|
100
|
ปรับฮีพ
|
2
|
1
|
3
|
7
|
17
|
19
|
25
|
36
|
100
|
8. สลับ 2 กับ 1
|
1
|
2
|
3
|
7
|
17
|
19
|
25
|
36
|
100
|
ปรับฮีพ
|
1
|
2
|
3
|
7
|
17
|
19
|
25
|
36
|
100
|
สิ้นสุดการเรียงลำดับ
|
1
|
2
|
3
|
7
|
17
|
19
|
25
|
36
|
100
|
การเรียงลำดับแบบผสาน(Merge Sort)
เป็นขั้นตอนวิธีในการเรียงลำดับที่อาศัยการเปรียบเทียบ และยังเป็นตัวอย่างขั้นตอนวิธีที่ใช้หลักการแบ่งแยกและเอาชนะทำให้ชั้นตอนวิธีนี้มีประสิทธิภาพ O(n log n) ในการอิมพลิเมนต์เพื่อการใช้งานจริง ๆ นั้นสามารถทำได้ทั้งแบบบนลงล่าง (Top-down) และแบบล่างขึ้นบน (Bottom-up) อนึ่งในการอิมพลิเมนต์โดยทั่วไปแล้วการเรียงแบบนี้จะไม่ศูนย์เสียลำดับของข้อมูลที่มีค่าเท่ากัน นั่นคือเป็นการเรียงที่เสถียร
ขั้นตอนวิธีอาศัยหลักการแบ่งแยกและเอาชนะและการเวียนบังเกิด โดยมีรายละเอียดดังนี้
- (ขั้นตอนการแบ่ง) สมมติว่ามีข้อมูลอยู่ n ชุด
- ถ้ามีข้อมูลแค่ 1 ชุด นั่นคือข้อมูลนั้นเรียงลำดับแล้ว
- ถ้ามีข้อมูลมากกว่านั้น ให้แบ่งเป็นสองส่วน แล้วทำการเวียนบังเกิด
- (ขั้นตอนเอาชนะ) เมื่อถึงขั้นตอนนี้จะได้ข้อมูลสองส่วน (โดยที่แต่ละส่วนเรียงในส่วนของตัวเองเรียบร้อยแล้ว) ทำการรวมข้อมูลทั้งสองส่วนนั้นให้เป็นข้อมูลก้อนเดียวที่ทั้งก้อนนั้นเรียงลำดับแล้ว ในการเรียงลำดับข้อมูลทั้งสิ้น n ชุด การเรียงลำดับแบบผสาน มีประสิทธิภาพในกรณีดีที่สุด (โดยมิได้ใส่เงื่อนไขพิเศษ) กรณีเฉลี่ย และกรณีแย่สุด เท่ากันคือ O(n log n) โดยจะแสดงให้ดูดังนี้ สมมติให้เวลาที่ใช้ในการเรียงข้อมูล n ชุด แทนด้วย T(n) เนื่องจาก การเรียงลำดับแบบผสาน มีสองขั้นตอนโดยขั้นแรกคือการแบ่งเป็นสองส่วนซึ่งสามารถทำได้ในเวลาคงที่แต่จะต้องเวียงบังเกิดเรียกตัวเองลงไปแก้ปัญหาที่เล็กลงครึ่งหนื่งสองปัญหา จะได้ว่าในส่วนแรกใช้เวลา 2T(n/2) และขั้นที่สองซึ่งเป็นการผสานข้อมูลสองชุดที่เล็กกว่า (ที่เรียงในตัวเองแล้ว) เป็นข้อมูลชุดใหญ่จะใช้เวลาอีก n ดังที่ได้แสดงให้ดูในตัวอย่างการอิมพลิเมนต์ด้านบน เมื่อรวมทั้งสองขั้นแล้วจะใช้เวลาทั้งสิ้น T(n) = 2T(n/2) + n หากใช้ Master Theorem ในการวิเคราะห์สมการนี้จะได้ผลลัพทธ์เป็น O(n log n) ดังที่ได้กล่าวไว้
